
Из истории развития математического моделирования результатов боевых действий
Н. ПЕДЕНКО, доктор военных наук, профессор, полковник в отставке
История в широком смысле этого слова не только интересна, но и поучительна в плане развития события или процесса на новом историческом витке. Рассматривая вопросы совершенствования тактики общевойсковых формирований Сухопутных войск (СВ) и влияние на ее развитие вооружения и техники, вспоминается время конца 70-х — начала 80-х годов прошлого века. Это был период, когда на вооружение Советской армии, в том числе и ее СВ, поступали новейшие образцы оружия и военной техники: танки, БМП (БМД), БТР, стрелковое оружие, противотанковые средства, ракетно-артиллерийские системы, средства ПВО, инженерная техника, системы управления войсками различного уровня. Этот список можно продолжать, но вопрос не в номенклатуре, а в существенном повышении уровня боевых свойств новой техники, прежде всего огневой мощи, живучести, подвижности, управления и ресурсных возможностей, что потребовало пересмотра всей системы боевой подготовки, способов ведения боевых действий и методов управления войсками.

Основу процесса решения всего комплекса отмеченных выше задач составляют вопросы оценки эффективности функционирования как отдельных систем вооружения и техники, так и боевых действий воинских формирований различного тактического уровня, оснащенных этим вооружением.
Необходимо отметить, что вопрос исследования боевых действий на основе математических методов возник не спонтанно. Уже в период Второй мировой войны значительно расширилась номенклатура и число типов применяемых в бою средств вооруженной борьбы и изменился характер боевых действий. Именно в этот период и возникла настоятельная необходимость использования численной оценки эффективности боевых действий, отличных от теории динамики средних, которая тогда была превалирующей и по существу единственной [1]. В этот период были разработаны методы оценки уязвимости целей и даже был создан особый математический аппарат для анализа конфликтных ситуаций, столь характерных для вооруженной борьбы [2].
Наряду с развитием общей теории боевой эффективности в послевоенный период активно разрабатывались вопросы оценки эффективности комплексного огневого поражения противника, необходимость в развитии которых диктовалась поиском более совершенной структуры и способов огневого поражения противника, уточнения нормативов по степени его поражения, расходу боеприпасов, времени решения огневых задач и т.д.
Однако, несмотря на интенсивное развитие общей теории боевой эффективности, и в частности теории эффективности огневых средств, практического применения в войсках они не имели. Объяснялось это сложностью и громоздкостью расчетов, которые проводились вручную.
Таким образом, на рубеже отмеченного времени возникло противоречие между возросшими боевыми возможностями войск и малоэффективным их использованием в новых высокодинамичных условиях ведения боевых действий. Потребность в прогнозировании результатов боя и огневого поражения противника стала насущной необходимостью. Требовалось не просто проводить отдельные расчеты, а определять тенденции и закономерности развития тактики общевойскового боя, обосновывать новые и совершенствовать существующие тактические принципы, исследовать влияние различных факторов на результаты боя, что требовало проведения массовых расчетов и множества итераций для одних и тех же расчетов, так как исследовались случайные процессы, характерные для стрельбы и ведения боевых действий.
Инструментом проведения этих массовых расчетов становилась электронная вычислительная техника, которая интенсивно развивалась. Персональных компьютеров в этот период еще не было, а стационарные ЭВМ для войск были несбыточной мечтой. Появление программируемых калькуляторов на вновь созданной в Военной академии имени М.В. Фрунзе кафедре вооружения и стрельбы восприняли с энтузиазмом, так как для них можно было создать программу на 94–106 шагов, которая позволяла бы рассчитывать основные показатели эффективности огня всей номенклатуры вооружения общевойсковых подразделений и частей. Однако появившаяся надежда ушла так же быстро, как и появилась. Тогда для определения одного из основных показателей эффективности огня — вероятности попадания в цель — использовалась формула вероятности ошибок в заданных пределах [3]:

(1)
где: — приведенная ширина цели, м;
— приведенная высота цели, м;
Кф — коэффициент фигурности цели, б/р;
— суммарные срединные ошибки стрельбы по направлению и высоте соответственно на i-й дальности, м;
Ф (X) — приведенная функция Лапласа, которая определяется по таблицам.
Применение таблиц для определения значений функции Лапласа не позволяло автоматически рассчитывать показатели эффективности стрельбы огневых средств ввиду ограниченного объема памяти программируемого калькулятора. Второй способ для расчета значений интегральной функции Лапласа методом численного интегрирования также был невозможен.
Руководитель кафедры П.В. Грень. поручил мне за два месяца найти решение этой задачи. Уже спустя месяц мной была представлена программа, которая позволяла автоматически рассчитывать основные показатели эффективности огня всей номенклатуры огневых средств общевойсковых подразделений на программируемом калькуляторе. На первый взгляд выведенная мной формула определения вероятности попадания выглядела более громоздкой, чем та, которую мы использовали на практике, но она была реализуема в программируемом калькуляторе:
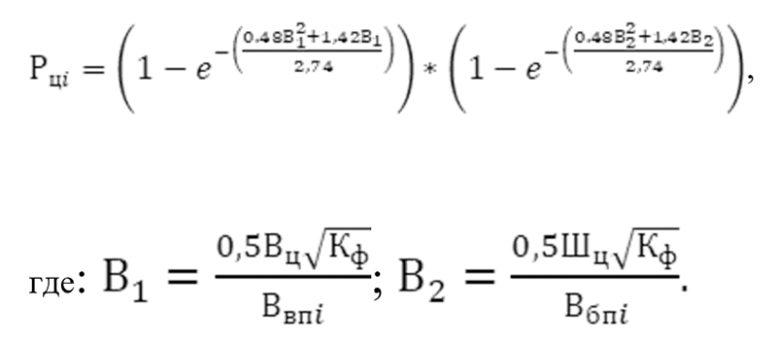
где: ;
Для демонстрации степени совпадения результатов при расчете по данной формуле и по таблице приведенной функции Лапласа мной был представлен график вероятности попадания, рассчитанной различными способами (рис. 1). Комментировать его мне не пришлось. Результат говорил сам за себя.
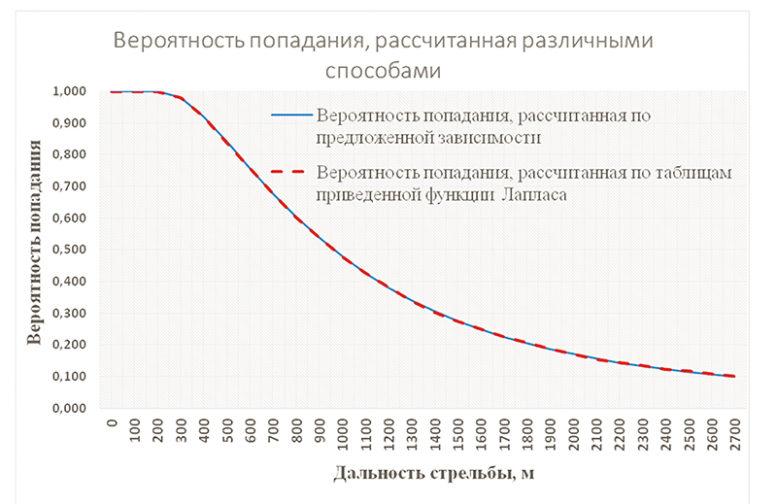
Рис. 1. График вероятности попадания в функции дальности стрельбы
Достоинством предложенной зависимости является использование показательной функции с аргументами (В1 и В2), которые, в свою очередь, являются функцией тех же параметров, что и в формуле вероятности ошибок в заданных пределах (1). При расчете вероятности попадания в площадную цель в качестве исходных данных берутся размеры площади цели и суммарные срединные ошибки стрельбы по направлению и дальности.
Благодаря предложенной зависимости вопросы учета эффективности огня системы вооружения общевойсковых формирований СВ удалось перевести из чисто теоретической плоскости в практическую. Сегодня с уверенностью можно утверждать, что именно это время было началом внедрения на кафедре цифровых технологий. В Военной академии имени М.В. Фрунзе слушатели выполняли курсовую работу, в которой исследовали влияние различных факторов на результаты огня и рассчитывали подготовительные упражнения стрельб для новой техники. При отработке вопросов полковой тематики по тактике слушатели обосновывали свои решения с учетом изменившихся боевых возможностей техники и вооружения в различных видах и условиях боя.
При этом следует заметить, что если вначале для расчета эффективности огня использовался только программируемый калькулятор, то уже с середины 80-х активно использовались персональные компьютеры, что значительно расширило объем, содержание и скорость решения расчетных задач.
В тот период академия привлекалась для разработки нового курса стрельб мотострелковых и танковых подразделений. Расчеты по обоснованию упражнений стрельб проводились преподавателями с использованием компьютерных программ, разработанных на кафедре. Автором статьи было разработано и издано учебное пособие, в котором раскрывались не только вопросы программы обучения слушателей по данной тематике с использованием электронной вычислительной техники, но и предлагалась методика расчета и построения номограмм, которые можно было применять в войсках для определения показателей эффективности огня конкретных образцов вооружения в условиях ограниченного времени [4]. B последующем автором было разработано и запатентовано устройство, напоминающее собой логарифмическую линейку, для определения показателей эффективности огня оружия общевойскового подразделения без проведения расчетов [5].
После довольно длительного периода стагнации на вооружение Российской армии стала поступать новая техника. При этом, наряду с совершенствованием традиционных систем вооружения СВ, разрабатываются принципиально новые. Это оружие на новых физических принципах (лазерное, лучевое), роботизированные и беспилотные средства поражения и средства управления с элементами искусственного интеллекта. История повторяется, но на качественно новом уровне.
Сегодня исследования эффективности огня новых перспективных систем вооружения является необходимым, но уже недостаточным условием, обеспечивающим развитие самой системы вооружения и тактики общевойсковых формирований СВ. Обоснованный прогноз развития тактики боевых действий требует комплексного анализа функционирования сложных структурно изменяющихся систем, одной из которых является общевойсковой бой. Эффективным методом решения этих задач, в том числе и исследования динамичных взаимосвязей между протекающими в бою процессами, является моделирование боевых действий [6].
Основу математической модели общевойскового боя составляет моделирование процесса огневого противоборства сторон как в ближнем, так и в дальнем огневом бою. Одной из задач в этом процессе является определение факта попадания в цель или в зону, в пределах которой возможно поражение цели для любого огневого средства независимо от его принципа поражения. Другими словами, определение вероятности попадания в цель является непременным условием для всех математических моделей поражения целей. Именно это определяет актуальность предложенной выше формулы и в настоящее время, несмотря на то, что сегодня возможности вычислительной техники значительно расширились.
Объясняется это тем, что характеристикой нормального закона выступает средняя квадратическая ошибка, а в теории стрельбы за основную характеристику кучности, точности и меткости стрельбы принята срединная ошибка. Исследования факторов, сопровождающих стрельбу и влияющих на нее, ведется через срединные ошибки. Кто-то может возразить, что срединная и среднеквадратическая ошибки связаны между собой через соответствующий коэффициент, и вероятность попадания может определяться по нормальному закону через срединную ошибку. Это действительно так. Но программа расчета вероятности попадания для ЭВМ на основе предлагаемой зависимости имеет преимущество прежде всего в упрощении алгоритма при сохранении необходимой точности расчетов, а как следствие — и в скорости решения задачи, и в рациональном использовании имеющегося объема компьютерной памяти, что очень важно при моделировании общевойскового боя в целом, где необходимо проводить сотни, а то и тысячи итераций по каждому виду оружия и возможных их сочетаниях в организационных структурах, а также учитывать параллельность процессов общевойскового боя в реальной системе без потери существенной информации о ней. В пользу такого подхода говорит и то, что в требованиях к модели общевойскового боя очень жестко стоит вопрос минимизации общего времени моделирования боя.
Важность учета эффективности огня средств вооружения СВ всех типов при исследовании общевойскового боя подтверждает анализ графических зависимостей, представленных на рисунке 2.
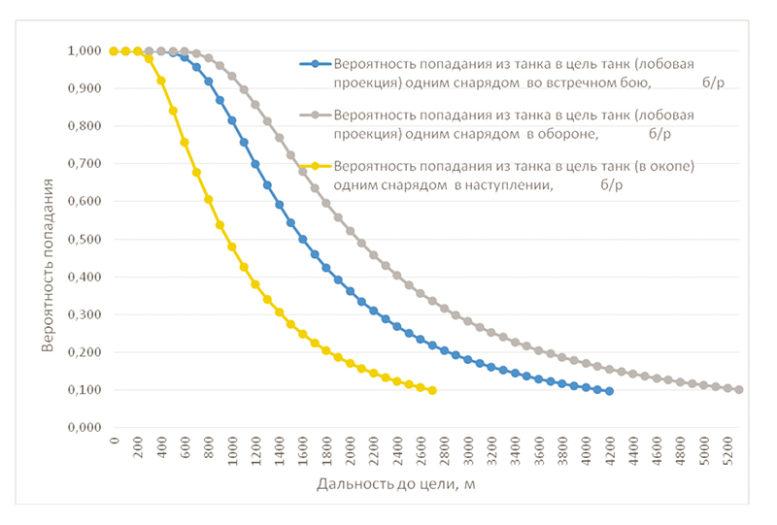
Рис. 2. График вероятности попадания гипотетического танка по танку в различных видах боя
Здесь наглядно показаны существенные различия в эффективности огня на одной и той же дальности в различных видах боя для одних и тех же средств. При этом приведено изменение только одного показателя — вероятности попадания в функции дальности. А если учесть, что вероятность попадания является основным аргументом для ряда других показателей, таких как надежность поражения, расход боеприпасов и времени для решения огневых задач, то вполне очевидна потребность в знании их значений в конкретной боевой обстановке и учете при организации и ведении боевых действий.
Эта история является наглядным примером творческого поиска решений в процессе профессиональной деятельности офицеров-управленцев. Раскрывает эволюцию развития вопросов оценки боевой эффективности систем вооружения и войсковых формирований тактического уровня СВ и пути ее дальнейшего совершенствования для проведения исследований в тактике уже на новом научно-техническом уровне развития цифровых технологий с помощью математической модели общевойскового боя, в которой может использоваться математическая зависимость определения вероятности попадания при моделировании процессов поражения цели любым видом оружия (традиционных систем и построенных на новых физических принципах), как состоящего на вооружении, так и перспективных отечественных и зарубежных образцов.
ЛИТЕРАТУРА:
Осипов М.П. Влияние численности сражающихся сторон на их потери. // Военный сборник. — 1915. — № 6. — С. 59–74.
Колмогоров А.Н. Число попаданий при нескольких выстрелах и общие принципы оценки эффективности систем стрельбы: Труды математического института им. В.А. Стеклова. — М.: Изд-во АН СССР, 1945. — С. 56.
Романов Н.И. Теория стрельбы из танков. — М.: ВА БТВ, 1973. — 426 с.
Педенко Н.П. Теоретические основы боевого применения вооружения танков, БМП (БТР) и стрелкового оружия в различных видах боя. — М.: ВАФ, 1989. — 94 с.
Педенко Н.П. Авторское свидетельство № 1832627 «Устройство определения эффективности стрельбы огневых средств».
Иванов С.С. Методологические основы описания процессов общевойскового боя при имитационном моделировании. / С.С. Иванов, Н.П. Педенко, О.С. Таненя // Военная мысль — 2020. — № 3. — С. 74–83.
